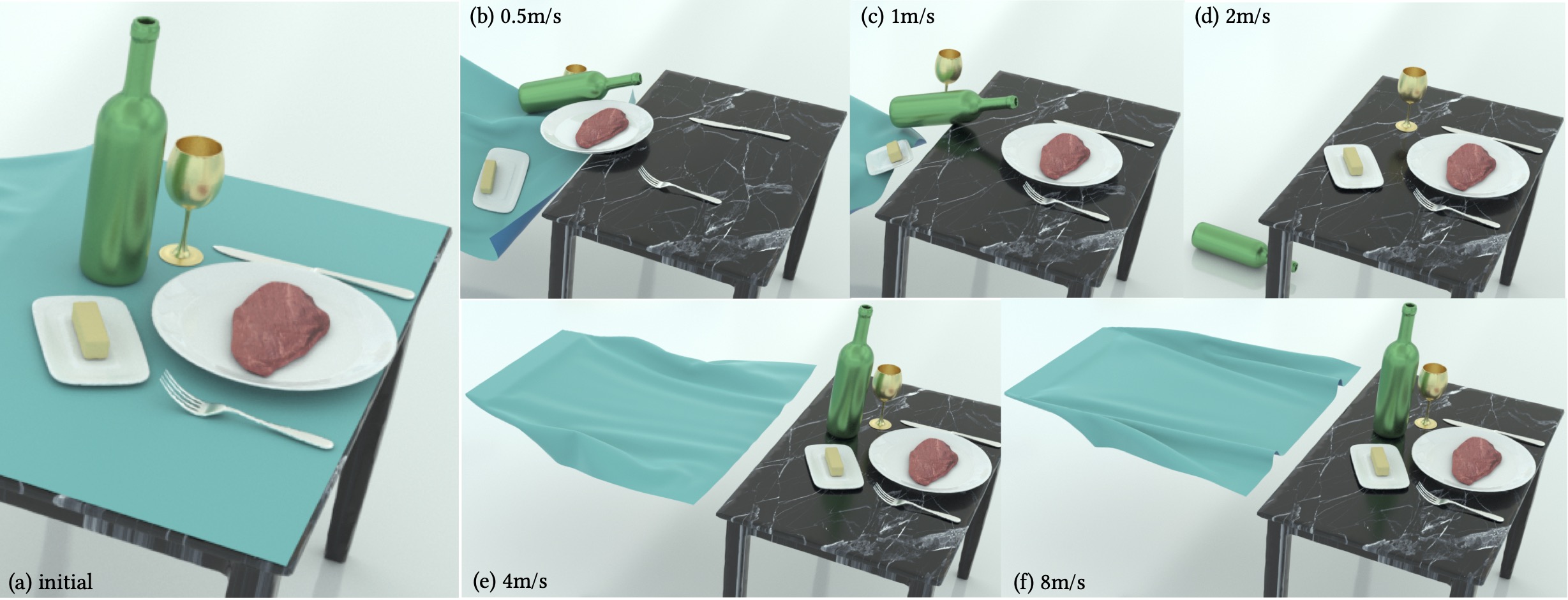
Table cloth pull: C-IPC enables high-rate time stepping of codimensional models with intersection-free, accurate, controllable strain-limiting, thickness modeling, and frictional contact. Here, stepping shell and volumetric FE models at h=0.01s, a square cloth is laid on a table with heavy, stiff volumetric dinnerware (a). C-IPC stably responds to rapid pulling at varying speeds (b-f) without stretching beyond limits while accurately resolving tight contacts between table edges and dinnnerware. With a slower pull in (b) of 0.5m/s nearly all objects pull off due to friction. As pull speed increase at 1m/s (c) and 2m/s (d), less dinnerware fall off with some just pulled a bit. In (e) and (f) pulling at higher speeds 4m/s or 8m/s leaves the stetting on table with rapid acceleration overcoming friction. Here too, combined strain-limiting and resolution of elastodynamics generates detailed wrinkling behaviors in the cloth for these faster pulls as it flies off the table.
We extend the incremental potential contact (IPC) model [Li et al. 2020] for contacting elastodynamics to resolve systems composed of arbitrary combinations of codimensional degrees-of-freedoms. This enables a unified, interpenetration-free, robust, and stable simulation framework that couples codimension-0,1,2, and 3 geometries seamlessly with frictional contact. Extending the IPC model to thin structures poses new challenges in computing strain, modeling thickness and determining collisions. To address these challenges we propose three corresponding contributions.
First, we introduce a C2 constitutive barrier model that directly enforces strain limiting as an energy potential while preserving rest state. This provides energetically consistent strain limiting models (both isotropic and anisotropic) for cloth that enable strict satisfaction of strain-limit inequalities with direct coupling to both elastodynamics and contact via minimization of the incremental potential.
Second, to capture the geometric thickness of codimensional domains we extend IPC to directly enforce distance offsets. Our treatment imposes a strict guarantee that mid-surfaces (respectively mid-lines) of shells (respectively rods) will not move closer than applied thickness values, even as these thicknesses become characteristically small. This enables us to account for thickness in the contact behavior of codimensional structures and so robustly capture challenging contacting geometries; a number of which, to our knowledge, have not been simulated before.
Third, codimensional models, especially with modeled thickness, mandate strict accuracy requirements that pose a severe challenge to all existing continuous collision detection (CCD) methods. To address these limitations we develop a new, efficient, simple-to-implement additive CCD (ACCD) method that applies conservative advancement [Mirtich 1996; Zhang et al. 2006] to iteratively refine a lower bound for deforming primitives, converging to time of impact.
@article{Li2021CIPC,
author = {Minchen Li and Danny M. Kaufman and Chenfanfu Jiang},
title = {Codimensional Incremental Potential Contact},
journal = {ACM Trans. Graph. (SIGGRAPH)},
year = {2021},
volume = {40},
number = {4},
articleno = {170}
}
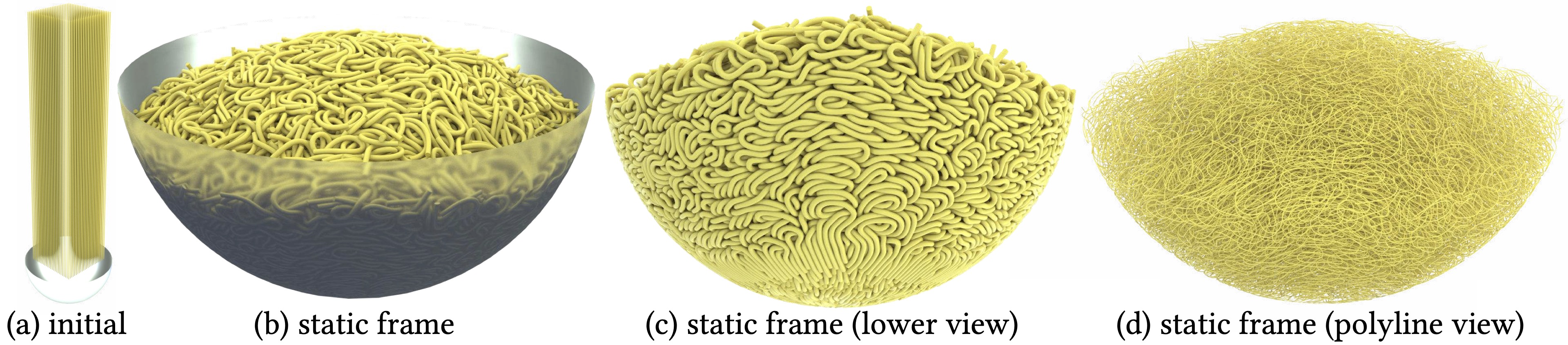
Noodles. (a) We drop 625 40cm-long noodles, modeled by discrete rods with C-IPC offset, into a bowl. (b) We set offset and dhat to model noodle thickness enabling the bowl to fill when they reach equilibrium. (c) We then remove the bowl to show the final intertwined, intersection-free configuration, noting that thickness offsets are satisfied throughout. In (d) we then remove the volume render to highlight the geometry is simulated solely with discrete rods polyline geometry.

"Precision" card shuffle. We divide fifty-four playing cards into two separate piles and bend them in preparation for a "precision" bridge shuffle. Unlike a human-performed bridge finish, where cards begin interleaved, here we increase challenge by keeping the two bridged piles apart and then (a) precisely, one-by-one, bottom up they are rapidly released in turn to shuffle the deck (b). We partially square the deck in (c), obtaining a fully shuffled stack with non-intersecting, interleaved cards that is 15.4mm heigh and so well-matching the height of a standard deck (d).

Twisted cylinder. Testing thickness modeling, contact resolution and buckling under extreme and increasing stress we start twisting a 1m- wide cloth cylinder with 88K nodes, a thickness offset of 1.5mm and dhat of 1mm. Time-stepped at h = 0.04s, C-IPC quickly obtains interesting folds and soon after forms a thick central cylinder of wound cloth supported by C-IPC’s finite thickness offset (upper left). In contrast, (upper right) without C-IPC’s thickness offset the correct geometry can not form (nor can it later capture the material’s buckling behavior) further emphasizing the importance of consistent thickness modeling for shells. After 32.96s of further twisting, our offset-thickened cloth continues to support complex contact-driven behaviors including the final buckled geometry (bottom); see our supplemental video for the detailed trajectory.